The project
The ‘MathsInTerre’ Research Thinktank is a project financed by the French National Research Agency (ANR), hosted by the IHP and supported by the INSMI - CNRS, structures that realise the importance of reflecting on the subject of “Mathematics and the complexity of the Earth system”.
A rich world
Mathematics is a fundamental discipline that has always been at the heart of important issues relating to the complexity of the Earth and, more especially, the environment. Understanding research issues as well as problems of sustainable management requires the adaptation of mathematical techniques in interaction with other disciplines. However, seeking solutions to environmental problems can also give rise to the development of new mathematical theories. These essential exchanges between disciplines gradually lead to a better understanding of the complexity of the world we live in.
What does a mathematician do?
During our discussions with non-mathematician communities, questions were often raised about mathematics that at first appeared naïve. Here, we would like to remind readers what mathematics is and what it does, basing our observations on the important work of learned societies and the initiative entitled “Mathematics of Planet Earth 2013”.
Mathematics in the real world
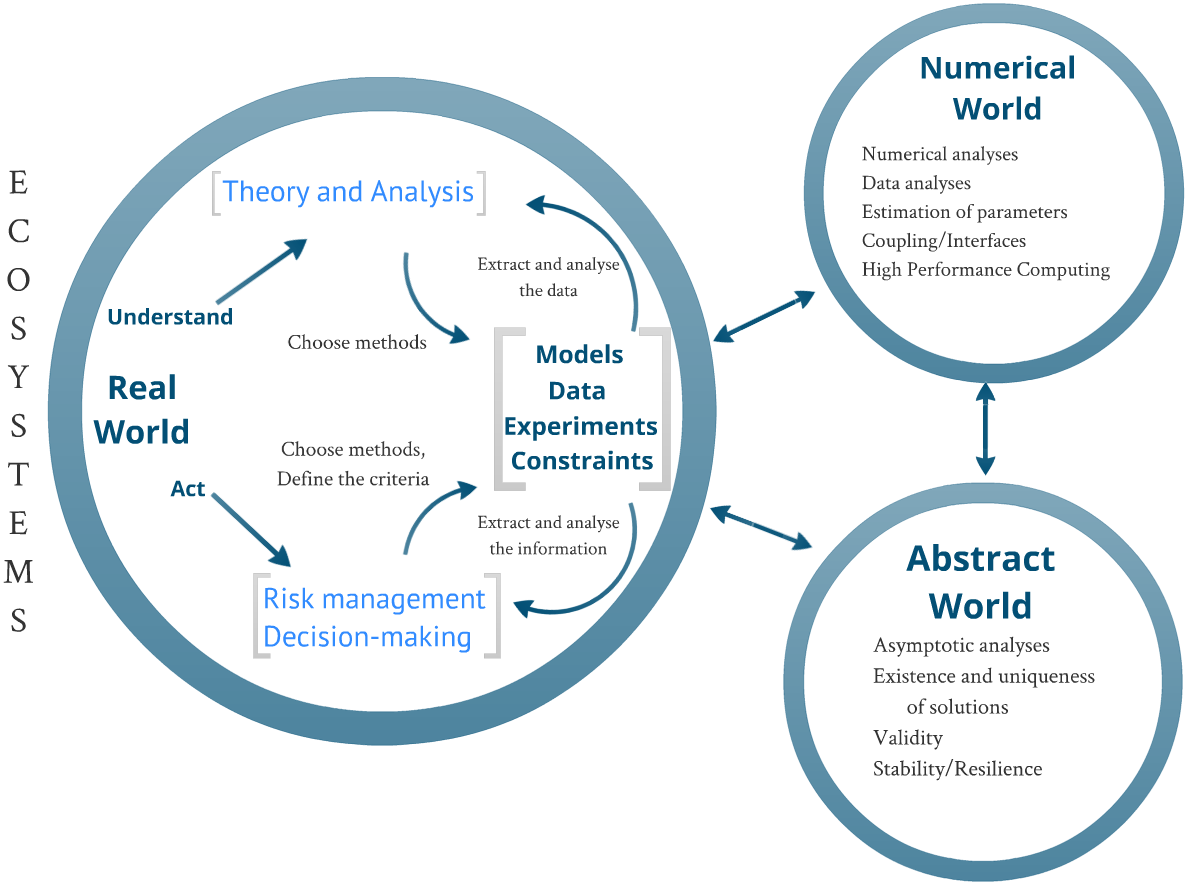
Acting as an aid to understanding, forecasting or decision-making, mathematics is like a very practical toolbox. However, it does have some shortcomings: a few mis- or poorly-understood tools lie at the bottom of the box, some are still new because they are unusable, while others still have to be invented. It is therefore important to take particular care in maintaining the links between the real world, theory and computational science.
Emerging mathematics
In this section we focus on emerging theories. New environmental and societal issues call for a better understanding of numerous complex and highly heterogeneous behaviour patterns. Inspired by these challenges, mathematicians are formalising new questions and attempting to provide answers (see Mathematics in the real world) by digging deep into their mathematical culture. These answers sometimes require the development of new mathematics.
Numerical mathematics
Numerical mathematics maintains close links with theory. Going from one to the other is a daily sport for some mathematicians. Such mathematicians often focus on problems arising from applications: coupling of processes, model validation, parameterizations, high-performance computing (supercomputing) ... Forming a bridge between the abstract and the concrete, numerical mathematics has difficulties in finding its place in the world of research in France.



.jpg)
