What does a mathematician do?
During our discussions with non-mathematician communities, questions were often raised about mathematics that at first appeared naïve. Here, we would like to remind readers what mathematics is and what it does, basing our observations on the important work of learned societies and the initiative entitled “Mathematics of Planet Earth 2013”.
« “It’s a discipline that feeds on its links with the other sciences, with society and the industrial world, but one that is also enriched itself in doing so (translation).”
- Mathématiques, l’explosion continue.
What does a mathematician do?
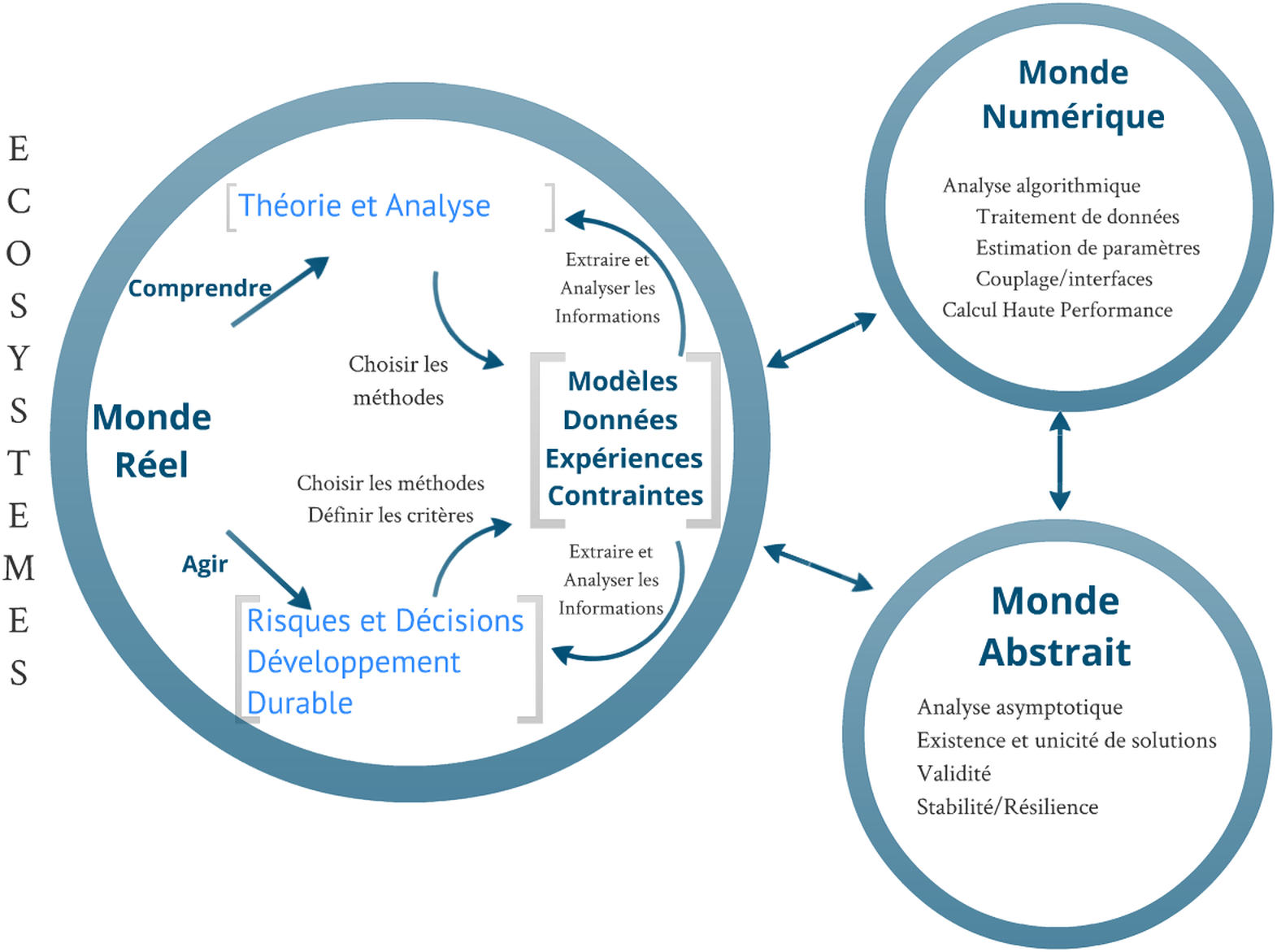
One of the mathematician’s roles is to observe the world and try to create conceptual tools to better understand it. All the power of mathematics lies in this two-fold approach: sometimes it can be used to resolve concrete problems, sometimes it develops very abstract and general methods that are disconnected from the real world but that – sometimes – have concrete and unexpected consequences. From the most abstract theories to the most concrete analytical methods, there is not a single mathematics but several! And they are all essential and intertwined. We have heard a lot about the rigour of the discipline but few people realise that the mathematician is, at the same time, flexible and open-minded! Indeed, the mathematician extends and adapts each of his or her objects of study to other applications and benefits from the links woven between different researchers in mathematics and other disciplines (in France and internationally). These links enable the mathematician to solve new problems.
Inspired by the text in Le Cercle, Les Echos d’E. Ghys (UMPA ENS Lyon).
What can mathematics contribute to environmental issues?
Mathematics is essential in everyday life. Thus, environmental and social issues that require the analysis, optimisation and management of increasingly complex systems result in a growing need for mathematics. This important role is well understood by certain countries, such as China and the United States, a fact that has been reflected in increased financial support for the discipline in these areas. Furthermore, the overall perception of the mathematician as being non-discriminatory and flexible enables him or her to play an important role in the dissemination of knowledge.« Mathematics … develops intuition, imagination, and a critical mind; it is also a universal language and a strong element of culture. (translation)» (in Mathématiques, l’explosion continue).
Why work in a theoretical and abstract manner? It doesn’t seem very useful!
It is this kind of typical remark that led to this page being written! It should be remembered that scientific progress in applied fields often comes about because of recent or past fundamental research (see Mathematics and the Earth: a long story).
It is important to keep in mind that « wishing to define activity or research in mathematics through its existing or potential applications would result in their disappearance. At the other end of the spectrum, favouring axiomatization, the study of structures and the internal dynamics of the discipline, as French mathematics did in the 1940-1970 period, albeit with considerable success, led to the development of so-called applied mathematics in France being held back (translation) » - Mathématiques, l’explosion continue.
Today many research mathematicians are involved in problems with concrete applications through exchanges and close collaboration with other disciplines. By way of example, mention may be made of initiatives such as the chair in Modélisation mathématique et biodiversité at the Polytechnique/MHN (Muséum national d’Histoire Naturelle) or the chair in Modélisation prospective at the CMA/ParisTech(Centre de Mathématiques Appliquées).
It is now important to focus on the Science-Earth link, treating it as a continuum, without any barriers between disciplines. It is questions arising from concrete issues that must determine the mathematics conducted in relation to the Earth, whether this is Mathematics in the real world, Numerical mathematics or Emerging mathematics. This question must become one of the essential criteria in determining the quality of applied mathematics.

