Le projet
L’Atelier de Réflexion Prospective « MathsInTerre » (ARP MathsInTerre) est un projet financé par l’Agence Nationale pour la Recherche (ANR), hébergé par l’IHP et soutenu par l’INSMI - CNRS, structures soucieuses de l’importance d’une réflexion sur le thème « Mathématiques et complexité du système Terre ».
Un monde riche
Les mathématiques sont une discipline fondamentale qui est, depuis toujours, au cœur d’enjeux importants liés à la complexité de la Terre, et plus particulièrement à l’environnement. Appréhender tant des problèmes de recherche que des problèmes de gestion durable requiert l’adaptation de techniques mathématiques en interactions avec d’autres disciplines, mais la recherche de solutions aux problèmes environnementaux peut également susciter le développement de nouvelles théories mathématiques. Ces allers retours essentiels apportent peu à peu une meilleure compréhension de la complexité du monde environnant.
Que fait un mathématicien ?
Lors de nos discussions avec les communautés non-mathématiciennes, des questions d’apparence naïve sur les mathématiques ont été posées plusieurs fois. Nous avons voulu rappeler ici ce que sont et font les mathématiques, en nous appuyant sur l’important travail des sociétés savantes et sur l’initiative Mathématiques de la Planète Terre 2013.
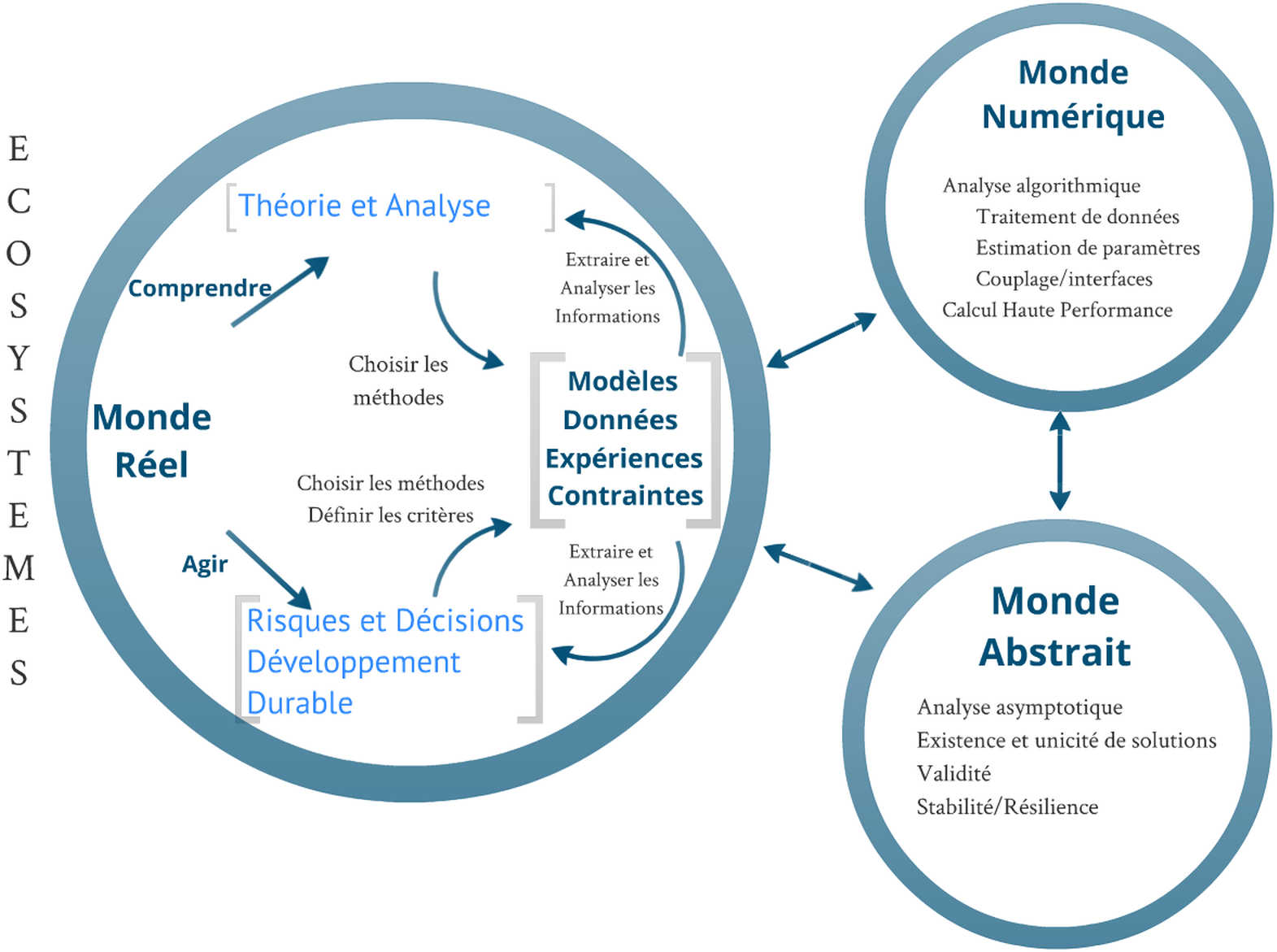
Mathématiques du monde réel
Aides à la compréhension, à la prévision ou à la décision, les mathématiques sont comme une boîte à outils bien pratique. Elle a tout de même des défauts : quelques outils incompris traînent au fond, certains sont restés comme neufs car inutilisables, d’autres encore seraient à inventer… Pour plus d'efficacité, il faut donc prendre un soin particulier à entretenir les liens entre le réel, la théorie et le numérique.
Mathématiques en émergence
Les nouvelles problématiques environnementales et sociétales demandent de mieux comprendre de nombreux comportements complexes fortement hétérogènes. Inspirés par ces problématiques, les mathématiciens formalisent de nouvelles questions et tentent d’en apporter des réponses (voir Mathématiques du monde réel) en puisant dans leur culture mathématique. Ces réponses nécessitent parfois le développement de nouvelles mathématiques.
Mathématiques du numérique
Ces mathématiques entretiennent des liens étroits avec la théorie. Passer de l’une à l’autre est un sport quotidien pour certains mathématiciens. Ces derniers s’intéressent souvent à des problèmes provenant des applications : couplage de processus, validation de modèles, paramétrisation, calcul haute performance ... Pont entre l’abstrait et le concret, les mathématiques numériques ont des difficultés à trouver leur place dans le monde de la recherche française.



.jpg)
